Real Time Kinematic (RTK) Solutions

RTK is where things get interesting, as this is where we can get down to centimeter level accuracy. RTK attempts to calculate the exact number of wavelengths between the satellites and the antenna of a fixed reference station in an attempt to provide either an RTK float or RTK integer solution. This process is known as ambiguity resolution. RTK integer solutions utilise an algorithm that will only yield a whole number of wavelengths, whereas an RTK float solution will allow for decimals. Typically RTK float is only used as a fallback solution in situations where an RTK integer solution cannot be found.

There are several considerations when implementing an RTK system:

• The absolute geographic accuracy of your system will depend on the accuracy of the base station location used for corrections, more on this here. If this reference station moves your rovers position will also move by the same amount unless the reference station’s location is reset. This can be an issue in some cases but I have also found it to be a benefit in others.
• Requirement for fixed local reference stations and communication infrastructure between rover and fixed station, or logging and post processing. If you are going to take on the cost and maintenance of this infrastructure then you should spend some time considering what the long term impacts of that will be.
• Accuracy typically falls off at a rate of around 1 PPM as a function of the distance between the rover and the local reference station. ie. 1 cm of accuracy is lost for every 10 km of distance.
• If you are utilising a commercial correction service (usually through an NTRIP provider) you will need a two way data connection in order to provide the service with an approximate location of your rover for matching with the nearest local reference station.
• There must be inter visibility of satellites between reference station and rover. As six satellites are required for an RTK solution this means that the same six usable satellites must be observable for the reference station and the rover at the same time, so make sure your reference station(s) have the best sky view possible if you are self managing these.

Absolute Geographic Accuracy vs. Other Forms of Accuracy

Typically I find that localisation solutions are required to be accurate to different reference true values, dependent on application.

1. It may be the case that you need absolute geographic accuracy to an existing datum so that you can incorporate external data sources, or have your data easily used by others.

2. Alternatively, maybe you need repeatable results, such that your rover always returns to the same place on repeated runs, but have no care for absolute geographic accuracy.

3. Another case might be that you have some other datum you need to be accurate against such as an independently sourced map or image.

In all three cases a high level of repeatability and accuracy is called for but the true value that we need to be accurate to has altered.

When operating using RTK position solutions we should take care with our reference station positions, as this is ultimately our shot on target. In this way it is better to think of RTK as providing centimetre level precision and repeatability, which could be accuracy too, depending on how well setup your local reference station is. If we are self-managing our base stations then it is up to us to decide what we want to be accurate to and how we are going to go about achieving this.

Accuracy Metrics

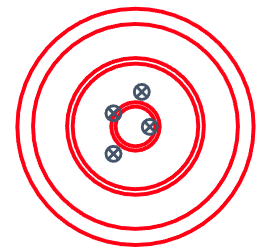
Circular Error Probable (CEP) is often the method used to quantify GNSS positioning errors. Typically we quote to a 50% CEP, ie. 50% of our observations fall within a circle of a given radius. If a receiver was reporting an accuracy of 0.8 m CEP then 50% of it’s observations would fall within a circle of radius 0.8 m. Another way to think of this is that the receiver will be within 0.8 m of the true measurement 50% of the time.

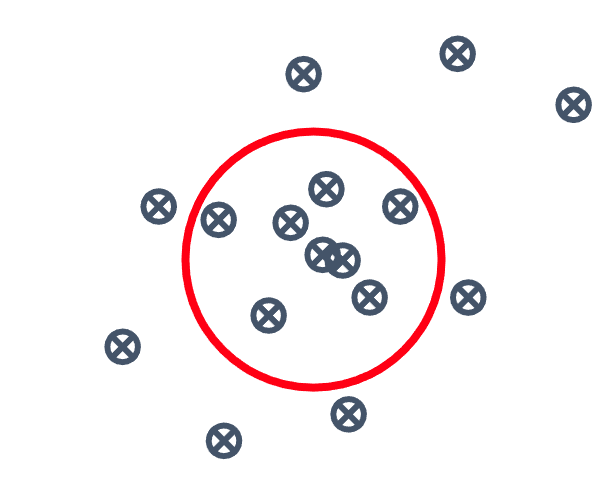
Figure 1: Circular Error Probable

An alternative, but often used approach is to utilise Root Mean Square Error (RMSE), where we take the square root of the average of the squared errors, typically quoted to one standard deviation (providing the mean is zero).

Dilution of Precision (DOP) is a measure of how well spaced the satellites that are currently being used in the localisation solution are. High values of DOP means that the satellites being utilised are close together in the sky, figure 2.

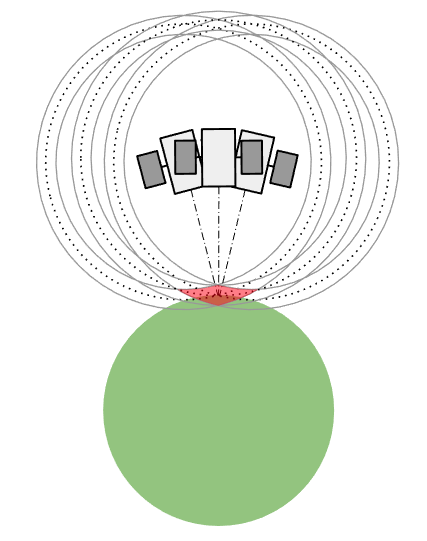
Figure 2: Poorly Spaced Satellites Yielding Poor DOP

This then leads to a less accurate solution than if the satellites being utilised were well spaced, figure 3.

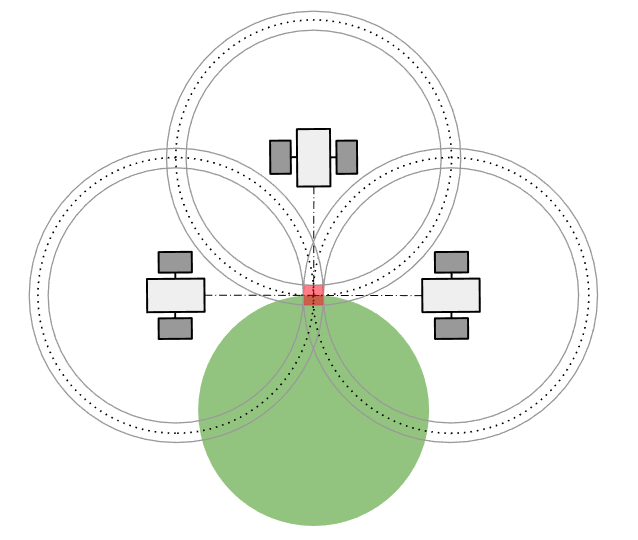
Figure 3: Well Spaced Satellites Providing Good DOP

Note that poor DOP usually comes as a result of ground level obstructions blocking the view of satellites that could have been utilised otherwise.

Resolution

When dealing with global frame coordinates, latitudes and longitudes, in decimal degrees you need to take care in preserving resolution across any stages in your processing. The number of decimal places used and your approximate latitude have an interplay that will effect the 2D positional accuracy you are able to achieve.

The data provided below is calculated based on the WGS84 model. It shows how variation of resolution effects differences in position, for a selection of latitudes. Northing and Easting here, being 2D components of position on the ground and have been combined to provide the 2D accuracy possible for each scenario.

For most applications utilising RTK integer solutions and centimetre level positioning eight or nine decimal places should provide enough head room.

An Intentionally Brief Word on Geodetic Models and Datums

When we are looking at accuracy it is worth taking some time to be sure that we are aware of what reference system we are measuring in, especially when comparing data from multiple sources. Most of the time these are configurable in your GNSS receiver, so it ought to be a case of selecting the one you need for your application, unless you are utilising a third party correction source. If this is the case then your end localisation solution will be in the datum of the correction source used. For the most part people have generally settled on WGS84 at the time of writing, however, NAD83 is still fairly pervasive in the USA so just take care, especially when using NTRIP providers.

• International - WGS84, ITRF00, ITRF 08
• USA - NAD83 - State plane system
• Europe - ETRS89
• UK - OSGB36

Standard Positioning Service

• Minimum Number of Satellites: Four (x, y, z, t)
• Expected Accuracy: ~1.5 m CEP

Differential GNSS

• Minimum Number of Satellites: Four (x, y, z, t)
• Expected Accuracy: ~45 cm CEP
• Differential Method: Code Phase

RTK Float

• Minimum Number of Satellites: Six (x, y, z, t, L1, L2)
• Expected Accuracy: ~20 cm CEP
• Differential Method: Carrier Phase
• Wavelength Ambiguity: Floating Point

RTK Integer

• Minimum Number of Satellites: Six (x, y, z, t, L1, L2)
• Expected Accuracy: ~1-2 cm CEP
• Differential Method: Carrier Phase
• Wavelength Ambiguity: Integer

Free Satellite Based Augementation Services (SBAS) - WAAS/ EGNOS/ MSAS/ GAGAN

• Minimum Number of Satellites: Six (x, y, z, t)
• Expected Accuracy: ~60-100 cm CEP
• Typically only contains corrections for GPS satellites
• Data not available worldwide
• Does not correct for local atmospheric and ionospheric conditions

Paid For Satellite Based Correction Services - Omnistar, Terrastar

• Minimum Number of Satellites: Six (x, y, z, t, L1, L2)
• Expected Accuracy: ~10 cm CEP
• Worldwide data
• Does not correct for local atmospheric and ionospheric conditions

Atmospheric and Ionospheric

Noise and delays due to having the GNSS signal travel through the atmosphere and ionosphere. As we are trying to estimate our position based on the time of flight for the GNSS signals, if the signal takes longer to reach us then our position will be inaccurate. However, these are typically constant over a given ground location and can be mitigated using RTK solutions.

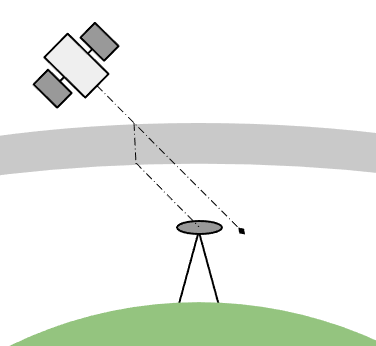
Figure 4: GNSS Error Induced by Atmospheric and Ionospheric Conditions

Space Segment Error

If the space segment is reporting satellite positions or time stamps incorrectly then this error will propogate into errors with the position solutions in the ground segment. Much like the atmospheric and ionospheric errors, these are typically constant over a given ground location and can be mitigated using RTK solutions.

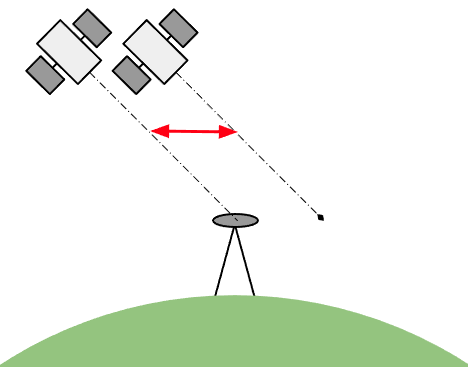
Figure 5: GNSS Error Due to Space Segment Errors

Multipath Reflections

Where the GNSS signal is reflected through an alternative path to the antenna. The alternate path will have a different time of flight and thus will cause position errors. Unlike the previous two error sources, these vary with the rovers pose, the surrounding environment and time, due to the changing geometry of the available GNSS satellites.

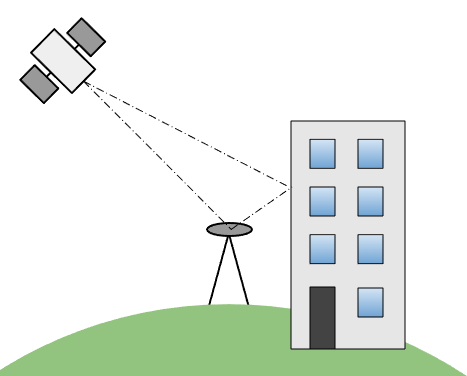
Figure 6: GNSS Error Due to Multipath Reflections

Antenna Selection

Generally antennas will come in an OEM style, without a radome cover and with a radome cover. Keep in mind that an antenna with a plastic radome cover will often have a different tuning to account for the radome versus it’s OEM style equivalent. If your application has it’s own outer cover it’s worth considering getting in touch with an antenna manufacturer to see if they can create a custom tuning for one of their OEM style antennas to work with your integrated cover. I know that this is a service that Tallysman used to offer, as well as several other manufacturers, I’m sure.

Broadly speaking, I would always try to utilise active antennas over passive ones, ideally with LNA gain greater than 17 dB. Built in multipath signal rejection and carrier phase linearity are good things to look out for when selecting antennas.

Antennas with a SAW filter can be utilised in environments where LTE or WiFi signals may cause some interference.

Below are a selection of antennas I have used in the past with good results, however, your selection will depend on how the antenna pairs with your GNSS receiver.

• Tallysman TW7000 and TW8000 Series
• U-Blox ANN-MB
• Novatel Vexxis 500 Series
• Novatel 700 Series

Ground Planes

A ground plane is a piece of material which is designed to block multipath reflections coming up from below the antenna. The material selection should be one that suits your application but it must block RF signals as much as is feasible.

The geometry of the ground plane is typically a thin disk. The diameter ought to be at least a half of the wavelength of the radio waves the antenna is receiving. L1 GNSS frequencies are ~1575 MHz, with L2 being ~1227 MHz. This leads to a minimum sized ground plane having a diameter of ~10 cm.

Electromagnetic Interference (EMI) and Carrier to Noise Ratio (CNR)

An integral component to the performance of a GNSS system is the sensitivity to the GNSS signals of the antenna and receiver pair. Carrier to noise ratio (CNR) is a common metric reported by GNSS receivers to indicate the performance of the hardware. CNR is the ratio of carrier power to noise power, normalised across a 1 Hz bandwidth.

CNR testing can be utilised to evaluate different GNSS receivers, antennas, ground planes, radomes and even to detect local sources of electromagnetic interference (EMI) that would disrupt GNSS signals. It is an indispensable tool for system integrators.

Many receivers also reject satellites with CNR levels below a particular threshold, determining that there is too much noise to provide a reliable solution. Typical limits are around 30-35 dB-Hz for L1 and 20-25 dB-Hz for L2, these values often can also be altered by the user, but do so with caution as you may end up with a worse solution as a result.

There are multiple tests that can be employed depending on what variable you are looking to see the impact of. I will outline two strategies that should highlight how you might go about constructing a test for a given scenario, but the TLDR is:

1. Log the CNR, usually through the NMEA GPGSV, GLGSV, GAGSV and GBGSV messages (constellation specific), and establish a base line reading
2. Change the hardware setup or run multiple setups in parallel at the approximate same location
3. Contrast the data recorded and make a judgment

Typical Results and Interpretation

I have provided a couple of example plots showing both time series CNR data, figure 7, and constellation positions, figure 8, as available from the NMEA GSV messages. When looking at these numbers it is important to keep in mind that dB-Hz is a logarithmic scale. Note that the observations that show up close to the horizon in figure 8 often have the lowest CNR (greatest noise) in figure 7. This is due to those signals typically traveling through more atmosphere and ionosphere due to there low elevation angle.

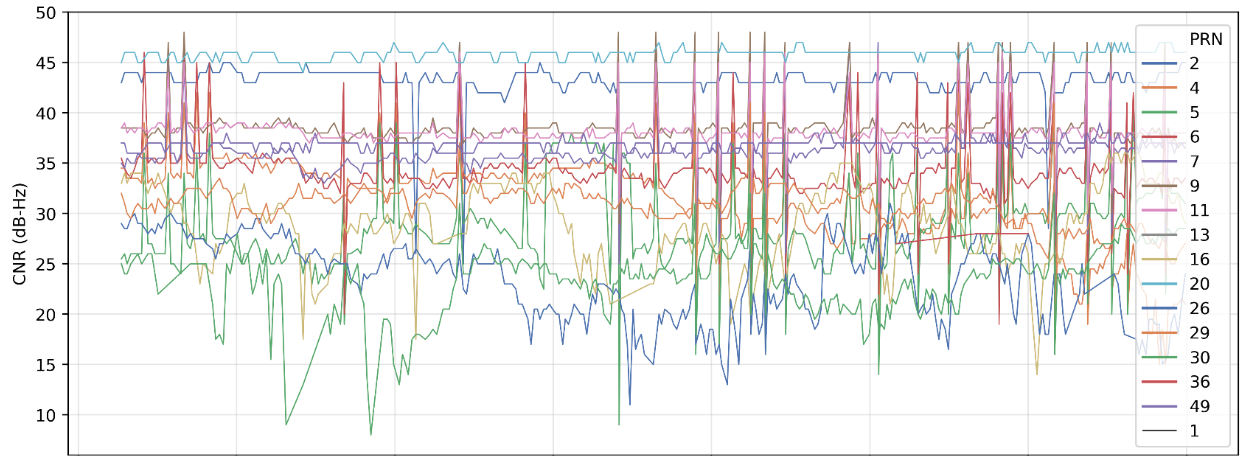
Figure 7: A Typical CNR Time Series Plot

Figure 8: A Typical Sky View Satellite Plot

When looking at the best three to five satellites from your data Tallysman say to interpret results in the following way “54dB is amazing, 53dB is excellent, 52dB is good and 49/50dB is ho-hum”. However, I imagine this is for a standalone GNSS receiver with a well tuned antenna, rather than a GNSS receiver integrated into a robotic platform or other vehicle, but this is still good for reference. Personally I have found that it is more reasonable to aim for 40-50 dB-Hz for L1 frequency signals and 35-40 dB-Hz for L2, but maybe I’m just “ho-hum” at doing this.

Communication Layer for Corrections

Serial radio modems are probably the most prolific method to transmit corrections from a self-managed local base station. These generally provide good range and reliability, however for many applications where other forms of connectivity are already available it often makes sense not to add the additional radio hardware.

For applications with data connections (WiFi, cellular, etc.) a software NTRIP (Network Transmission of RTCM over IP) client can be deployed, coupled with either a paid for subscription NTRIP service or self-managed NTRIP server connected to your own GNSS reference stations. The NTRIP protocol allows for two way communication between rovers and multiple base stations. This allows a rover to provide it’s approximate current location and request corrections from the station that is closest to it. NTRIP is worth investigating at if you are looking at working over very large areas (10+ km) or managing multiple base stations of your own.

Custom connections utilising TCP, UDP, DDS, MQTT, ZeroMQ, etc. for a communication transport layer, all make for fair alternatives to NTRIP, especially if you have local point to point connections, or some custom policies about which base stations you’d like rovers connect to. I have found that UDP provides the lowest latency and, given how reliable most modern networks are, packets are rarely dropped, and even when they are it typically isn’t an issue.

Correction packets can technically be considered as valid for as long as it the ionospheric and atmospheric conditions remain stable for, however, we generally have no idea if this is the case or not. As such, most GNSS receivers allow you to set a limit on how old a correction packet can be and still be utilised in it’s solution, this is often referred to as the “diff. age”. This value usually defaults to sixty second for most receivers. So if we are sending GNSS correction once every 2-10 seconds, we can afford to drop several packets before hitting this limit of sixty seconds. Ultimately you will need to do some testing and benchmarking of your connectivity to see what sort of frequencies and limits on diff. age make sense for your system.

Found this useful or interesting?

Consider donating to support.

Any question, comments, corrections or suggestions?

Reach out on the social links below through the buttons.